The periodic 3D-triangulation class of Cgal is designed to represent the triangulations of a set of points in the three-dimensional flat torus. The triangulation forms a partition of the space it is computed in. It is a simplicial complex, i.e. it contains all incident j-simplices (j<k) of any k-simplex and two k-simplices either do not intersect or share a common j-face, j<k. The occurring simplices of dimension up to three are called vertex, edge, facet, and cell, respectively.
37.1 The flat torus
The 3D Periodic Triangulation package computes triangulations in the space
c3, which is defined as follows: Let c ∈ ℝ \ {0} and G be the group (c ⋅ ℤ3, +), where
c ⋅ ℤ denotes the set containing all integer multiples of
c. The flat torus is the quotient space: c3:=ℝ3/G. The parameter c defines the period.
The elements of c3 are the equivalence classes of sets of
points in ℝ3. We call these points representatives
of an element of c3. The implementation works not directly on elements of c3 but on some representatives in ℝ3. So there need to
be distinguished representatives to work on. Given α, β,
and γ, the cube
[α,α+c) × [β,β+c) × [γ,γ+c)
contains exactly one representative of each element in c3. We call it original domain. From now on, when we talk
about points, we generally mean representatives of elements
of c3 that lie inside the original domain. Note that any
input point is required to be an element of the half-open cube
representing the original domain as defined above.
There are simplices containing points inside the original domain but
also points outside it. The points outside the original domain are
periodic copies of points inside the original domain. So, to
specify a simplex we need points together with some additional
information that determines the respective periodic copy of each point.
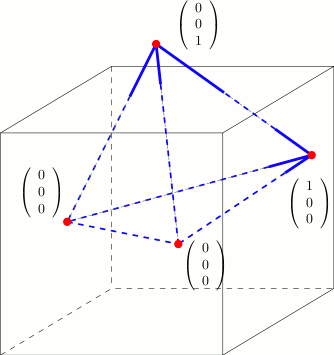
The set of representatives of an element of c3 is a cubic
point grid. We address each representative by a three-dimensional
integer vector (ox,oy,oz), called offset. It
represents the number of periods a representative in the original
domain must be translated in x-, y-, and z-direction.
The vector (0,0,0) corresponds to the representative in the original
domain. To specify a k-simplex we need k+1 point-offset pairs
(cf. Fig. 37.1).
37.2 Representation
A triangulation is a collection of vertices and cells that are linked together through incidence and adjacency relations. Each cell gives access to its four incident vertices, their corresponding offsets, and to its four adjacent cells. Each vertex gives access to one of its incident cells.
The four vertices of a cell are indexed with 0, 1, 2 and 3 in positive
orientation. The orientation of a simplex in c3 is
defined as the orientation of the corresponding simplex in ℝ3 given by representatives determined by the respective offsets
(see Figure 37.2).
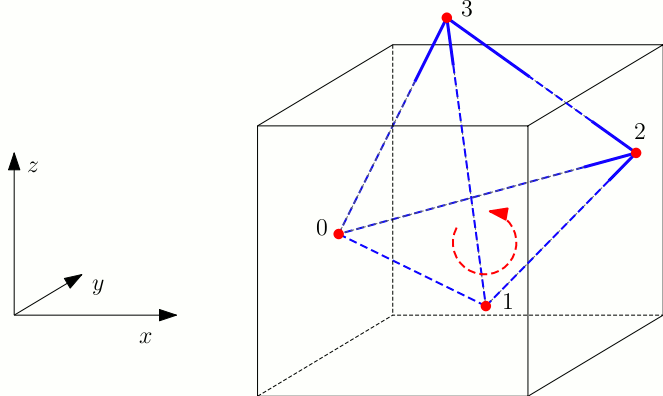
As in the underlying combinatorial triangulation (see Chapter 36), the neighbors of a cell are indexed with 0, 1, 2, 3 in such a way that the neighbor indexed by i is opposite to the vertex with the same index. Also edges (1-faces) and facets (2-faces) are not explicitly represented: a facet is given by a cell and an index (the facet i of a cell c is the facet of c that is opposite to the vertex with index i) and an edge is given by a cell and two indices (the edge (i,j) of a cell c is the edge whose endpoints are the vertices of c with indices i and j). See Figure 36.1.
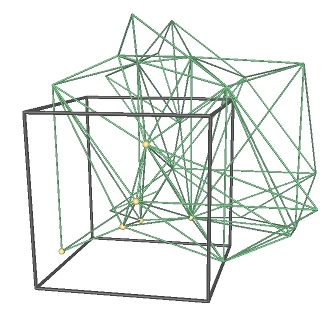
Some point sets do not admit a triangulation in c3. In
this case we use 27 periodic copies of the point set arranged in a
cube of edge length 3c. Any point set constructed in this way has a
triangulation in ℝ3/G' with G'=(3c ⋅ ℤ,+)
[CT09]. So we compute the triangulation in this
space, which is a 27-sheeted covering space of c3
(see Figure 37.3).
The machinery that manages the copies is largely hidden from the
user. However there are some effects that cannot be ignored. For
example if the point set does not permit a triangulation in c3 then the combinatorial iterators (Cell_iterator,
Facet_iterator, Edge_iterator, and Vertex_iterator)
return all simplices that are internally stored, which correspond to
27 periodic copies of each geometric primitive (Tetrahedron, Triangle,
Segment, and Point). This is necessary to ensure consistency in the
adjacency relations. In case it is desired to have only one periodic
copy of each primitive, we provide geometric iterators. They
return geometric primitives of the triangulation without relations
between them. Another effect is that when the algorithm switches from
27-sheeted covering to 1-sheeted covering the Vertex_handles and
Cell_handles referencing deleted items become invalid.
In the data structure each vertex stores the input point it
corresponds to. If we are computing in 27-sheeted covering
space, each vertex stores the representative inside the
original domain it corresponds to. So, the 27 vertices corresponding
to the same element of c3 all store the same
representative in ℝ3, and not different periodic copies.
Validity A periodic triangulation is said to be locally valid iff
(a)-(b) Its underlying combinatorial graph, the triangulation
data structure, is locally valid
(see Section 36.1 of Chapter 36)
(c) Any cell has its vertices ordered according to positive
orientation. See Figure 37.2.
37.3 Delaunay Triangulation
The class Periodic_3_Delaunay_triangulation_3 implements Delaunay triangulations of point sets in c3.
Delaunay triangulations have the empty sphere property, that is, the circumscribing sphere of each cell does not contain any other vertex of the triangulation in its interior. These triangulations are uniquely defined except in degenerate cases where five points are co-spherical. Note however that the Cgal implementation computes a unique triangulation even in these cases [DT03].
This implementation is fully dynamic: it supports both insertions of points and vertex removal.
37.4 Triangulation Hierarchy
The class Periodic_3_triangulation_hierarchy_3 is the adaptation of the hierarchical structure described in chapter 35 to the periodic case.37.5 Software Design
We have chosen the prefix ``Periodic_3'' to emphasize that the triangulation is periodic in all three directions of space. There are also ``cylindrical'' periodicities where the triangulation is periodic only in one or two directions of space.The two main classes Periodic_3_Delaunay_triangulation_3 and Periodic_3_triangulation_3 provide high-level geometric functionality and are responsible for the geometric validity. Periodic_3_Delaunay_triangulation_3 contains all the functionality that is special to Delaunay triangulations, such as point insertion and vertex removal, the side-of-sphere test, finding the conflicting region of a given point, dual functions etc. Periodic_3_triangulation_3 contains all the functionality that is common to triangulations in general, such as location of a point in the triangulation [DPT02], access functions, geometric queries like the orientation test etc.
They are built as layers on top of a triangulation data structure, which stores their combinatorial structure. This separation between the geometry and the combinatorics is reflected in the software design by the fact that the triangulation classes take two template parameters:
- the geometric traits class, which provides the type of points to use as well as the elementary operations on them (predicates and constructions). Furthermore it contains the offset type. The concept for this parameter is described in more detail in Section 37.5.1 and as the concept Periodic_3DelaunayTriangulationTraits_3 in the reference manual.
- the triangulation data structure class, which stores the combinatorial structure, described in Section 37.5.2 and in more detail in Chapter 36. The triangulation data structure needs models of the concepts Periodic_3TriangulationDSCellBase_3 and Periodic_3TriangulationDSVertexBase_3 as template parameters.
37.5.1 The Geometric Traits Parameter
The first template parameter of the Delaunay triangulation class Periodic_3_Delaunay_triangulation_3<Periodic_3DelaunayTriangulationTraits_3, TriangulationDataStructure_3> is the geometric traits class, described by the concept Periodic_3DelaunayTriangulationTraits_3. It is different to the DelaunayTriangulationTraits_3 (see chapter 35.5.1) in that it implements all objects, predicates and constructions with using offsets.The class Periodic_3_triangulation_traits_3<Traits,Periodic_3Offset_3> provides the required functionality. It expects two template parameters: A model of the concept DelaunayTriangulationTraits_3 and a model of the concept Periodic_3Offset_3.
The kernels Cartesian, Homogeneous, Simple_cartesian, Simple_homogeneous and Filtered_kernel can all be used as models for Traits. Periodic_3_triangulation_traits_3 provides exact predicates and exact constructions if Traits does. It provides exact predicates but not exact constructions if Filtered_kernel<CK> with CK an inexact kernel is used as its first template parameter. Using Exact_predicates_inexact_constructions_kernel as Traits provides fast and exact predicates and not exact constructions, using Exact_predicates_exact_constructions_kernel provides fast and exact predicates and exact constructions. The latter is recommended if the dual constructions and constructions of points, segments, triangles, and tetrahedra are used.
The second parameter Periodic_3Offset_3 defaults to Periodic_3_offset_3.
37.5.2 The Triangulation Data Structure Parameter
The second template parameter of the main classes Periodic_3_triangulation_3 and Periodic_3_Delaunay_triangulation_3 is a triangulation data structure class. This class can be seen as a container for the cells and vertices maintaining incidence and adjacency relations (see Chapter 36). A model of this triangulation data structure is Triangulation_data_structure_3, and it is described by the TriangulationDataStructure_3 concept. This model is itself parameterized by a vertex base class and a cell base class, which gives the possibility to customize the vertices and cells used by the triangulation data structure, and hence by the geometric triangulation using it. To represent periodic triangulations the cell base and vertex base classes need to meet the concepts Periodic_3TriangulationDSCellBase_3 and Periodic_3TriangulationDSVertexBase_3.
A default value for the triangulation data structure parameter is provided in all the triangulation classes, so it does not need to be specified by the user unless he wants to use a different triangulation data structure or a different vertex or cell base class.
37.5.3 Flexibility of the Design
Periodic_3_triangulation_3 uses the TriangulationDataStructure_3 in essentially the same way as Triangulation_3. That is why the flexibility described in 35.5 is applicable in exactly the same way. Also the classes Triangulation_vertex_base_with_info_3 and Triangulation_cell_base_with_info_3 can be reused directly, see also Example 37.6.2.1.37.6 Examples
37.6.1 Basic Example
This example shows the incremental construction of a 3D Delaunay triangulation, the location of a point and how to perform elementary operations on indices in a cell. It uses the default parameter of the Periodic_3_Delaunay_triangulation_3 class for the triangulation data structure.
File: examples/Periodic_3_triangulation_3/simple_example.cpp
#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Periodic_3_triangulation_traits_3.h>
#include <CGAL/Periodic_3_Delaunay_triangulation_3.h>
#include <iostream>
#include <fstream>
#include <cassert>
#include <list>
#include <vector>
typedef CGAL::Exact_predicates_inexact_constructions_kernel K;
typedef CGAL::Periodic_3_triangulation_traits_3<K> GT;
typedef CGAL::Periodic_3_Delaunay_triangulation_3<GT> PDT;
typedef PDT::Cell_handle Cell_handle;
typedef PDT::Vertex_handle Vertex_handle;
typedef PDT::Locate_type Locate_type;
typedef PDT::Point Point;
typedef PDT::Iso_cuboid Iso_cuboid;
int main()
{
Iso_cuboid domain(-1,-1,-1,2,2,2); // The cube for the periodic domain
// construction from a list of points :
std::list<Point> L;
L.push_front(Point(0,0,0));
L.push_front(Point(1,0,0));
L.push_front(Point(0,1,0));
PDT T(L.begin(), L.end(), domain); // Put the domain with the constructor
int n = T.number_of_vertices();
// insertion from a vector :
std::vector<Point> V(3);
V[0] = Point(0,0,1);
V[1] = Point(1,1,1);
V[2] = Point(-1,-1,-1);
n = n + T.insert(V.begin(), V.end());
assert( n == 6 ); // 6 points have been inserted
assert( T.is_valid() ); // checking validity of T
Locate_type lt;
int li, lj;
Point p(0,0,0);
Cell_handle c = T.locate(p, lt, li, lj);
// p is the vertex of c of index li :
assert( lt == PDT::VERTEX );
assert( c->vertex(li)->point() == p );
Vertex_handle v = c->vertex( (li+1)&3 );
// v is another vertex of c
Cell_handle nc = c->neighbor(li);
// nc = neighbor of c opposite to the vertex associated with p
// nc must have vertex v :
int nli;
assert( nc->has_vertex( v, nli ) );
// nli is the index of v in nc
std::ofstream oFileT("output",std::ios::out);
// writing file output;
oFileT << T;
PDT T1;
std::ifstream iFileT("output",std::ios::in);
// reading file output;
iFileT >> T1;
assert( T1.is_valid() );
assert( T1.number_of_vertices() == T.number_of_vertices() );
assert( T1.number_of_cells() == T.number_of_cells() );
return 0;
}
37.6.2 Changing the Vertex Base
The following two examples show how the user can plug his own vertex base in a triangulation. Changing the cell base is similar.
Adding a Color
If the user does not need to add a type in a vertex that depends on the TriangulationDataStructure_3 (e.g. a Vertex_handle or Cell_handle), then he can use the Triangulation_vertex_base_with_info_3 class to add his own information easily in the vertices. The example below shows how to add a CGAL::Color this way.
File: examples/Periodic_3_triangulation_3/colored_vertices.cpp
#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Periodic_3_triangulation_filtered_traits_3.h>
#include <CGAL/Periodic_3_Delaunay_triangulation_3.h>
#include <CGAL/Triangulation_vertex_base_with_info_3.h>
#include <CGAL/IO/Color.h>
typedef CGAL::Exact_predicates_inexact_constructions_kernel K;
typedef CGAL::Periodic_3_triangulation_filtered_traits_3<K> GT;
typedef CGAL::Periodic_3_triangulation_ds_vertex_base_3<> VbDS;
typedef CGAL::Triangulation_vertex_base_3<GT,VbDS> Vb;
typedef CGAL::Periodic_3_triangulation_ds_cell_base_3<> CbDS;
typedef CGAL::Triangulation_cell_base_3<GT,CbDS> Cb;
typedef CGAL::Triangulation_vertex_base_with_info_3<CGAL::Color, GT, Vb> VbInfo;
typedef CGAL::Triangulation_data_structure_3<VbInfo, Cb> TDS;
typedef CGAL::Periodic_3_Delaunay_triangulation_3<GT, TDS> PDT;
typedef PDT::Point Point;
int main()
{
PDT T;
T.insert(Point(0,0,0));
T.insert(Point(.1,0,0));
T.insert(Point(0,.1,0));
T.insert(Point(0,0,.1));
T.insert(Point(.2,.2,.2));
T.insert(Point(.9,0,.1));
// Set the color of finite vertices of degree 6 to red.
PDT::Vertex_iterator vit;
for (vit = T.vertices_begin(); vit != T.vertices_end(); ++vit)
if (T.degree(vit) == 6)
vit->info() = CGAL::RED;
return 0;
}
Adding Handles
If the user needs to add a type in a vertex that depends on the TriangulationDataStructure_3 (e.g. a Vertex_handle or Cell_handle), then he has to derive his own vertex base class, as the following example shows.
File: examples/Periodic_3_triangulation_3/periodic_adding_handles.cpp
#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Periodic_3_triangulation_filtered_traits_3.h>
#include <CGAL/Periodic_3_Delaunay_triangulation_3.h>
#include <CGAL/Periodic_3_triangulation_ds_vertex_base_3.h>
#include <CGAL/Triangulation_vertex_base_3.h>
template < class GT, class VbDS,
class Vb = CGAL::Triangulation_vertex_base_3<GT,VbDS> >
class My_vertex_base
: public Vb
{
public:
typedef typename Vb::Vertex_handle Vertex_handle;
typedef typename Vb::Cell_handle Cell_handle;
typedef typename Vb::Point Point;
template < class TDS2 >
struct Rebind_TDS {
typedef typename Vb::template Rebind_TDS<TDS2>::Other Vb2;
typedef My_vertex_base<GT, Vb2> Other;
};
My_vertex_base() {}
My_vertex_base(const Point& p)
: Vb(p) {}
My_vertex_base(const Point& p, Cell_handle c)
: Vb(p, c) {}
Vertex_handle vh;
Cell_handle ch;
};
typedef CGAL::Exact_predicates_inexact_constructions_kernel K;
typedef CGAL::Periodic_3_triangulation_filtered_traits_3<K> GT;
typedef CGAL::Periodic_3_triangulation_ds_vertex_base_3<> VbDS;
typedef CGAL::Periodic_3_triangulation_ds_cell_base_3<> CbDS;
typedef CGAL::Triangulation_cell_base_3<GT,CbDS> Cb;
typedef CGAL::Triangulation_data_structure_3<My_vertex_base<GT,VbDS>, Cb> TDS;
typedef CGAL::Periodic_3_Delaunay_triangulation_3<GT,TDS> PDT;
typedef PDT::Vertex_handle Vertex_handle;
typedef PDT::Point Point;
int main()
{
PDT T;
Vertex_handle v0 = T.insert(Point(0,0,0));
Vertex_handle v1 = T.insert(Point(.1,0,0));
Vertex_handle v2 = T.insert(Point(0,.1,0));
Vertex_handle v3 = T.insert(Point(0,0,.1));
Vertex_handle v4 = T.insert(Point(.2,.2,.2));
Vertex_handle v5 = T.insert(Point(.9,0,.1));
// Now we can link the vertices as we like.
v0->vh = v1;
v1->vh = v2;
v2->vh = v3;
v3->vh = v4;
v4->vh = v5;
v5->vh = v0;
return 0;
}
37.6.3 27-sheeted Covering
The user can check at any time whether a triangulation would be a simplicial complex in c3 and force a conversion if
so. However this should be done very carefully in order to be sure
that the internal structure always remains a simplicial complex and
thus a triangulation.
In this example we construct a triangulation that can be converted to the 1-sheeted covering. However, we can insert new points such that the point set does not have a Delaunay triangulation in the 1-sheeted covering anymore, so the triangulation is not extensible.
File: examples/Periodic_3_triangulation_3/covering.cpp
#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Periodic_3_triangulation_traits_3.h>
#include <CGAL/Periodic_3_Delaunay_triangulation_3.h>
#include <iostream>
#include <vector>
typedef CGAL::Exact_predicates_inexact_constructions_kernel K;
typedef CGAL::Periodic_3_triangulation_traits_3<K> GT;
typedef CGAL::Periodic_3_Delaunay_triangulation_3<GT> PDT;
typedef PDT::Point Point;
typedef PDT::Covering_sheets Covering_sheets;
int main()
{
PDT T;
// Input point grid (27 points)
for (double x=0. ; x < .9 ; x += 0.33) {
for (double y=0. ; y < .9 ; y += 0.33) {
for (double z=0. ; z < .9 ; z += 0.33) {
T.insert(Point(x,y,z));
} } }
Covering_sheets cs = T.number_of_sheets();
std::cout<<"Current covering: "<<cs[0]<<' '<<cs[1]<<' '<<cs[2]<<std::endl;
if ( T.is_triangulation_in_1_sheet() ) { // = true
bool is_extensible = T.is_extensible_triangulation_in_1_sheet_h1()
|| T.is_extensible_triangulation_in_1_sheet_h2(); // = false
T.convert_to_1_sheeted_covering();
cs = T.number_of_sheets();
std::cout<<"Current covering: "<<cs[0]<<' '<<cs[1]<<' '<<cs[2]<<std::endl;
if ( is_extensible ) // = false
std::cout<<"It is safe to change the triangulation here."<<std::endl;
else
std::cout<<"It is NOT safe to change the triangulation here!"<<std::endl;
T.convert_to_27_sheeted_covering();
cs = T.number_of_sheets();
std::cout<<"Current covering: "<<cs[0]<<' '<<cs[1]<<' '<<cs[2]<<std::endl;
}
std::cout<<"It is (again) safe to modify the triangulation."<<std::endl;
return 0;
}
37.6.4 Large Point Set
For large point sets there are two optimizations available. Firstly, there is spatial sorting that sorts the input points according to a Hilbert curve, see chapter 61.2. The second one inserts 36 appropriately chosen dummy points to avoid the use of a 27-sheeted covering in the beginning. The 36 dummy points are deleted in the end. If the point set turns out to not have a Delaunay triangulation in 1-sheeted covering, the triangulation is converted to 27-sheeted covering during the removal of the 36 dummy points. This might take even longer than computing the triangulation without using this optimization. In general, uniformly distributed random point sets of more than 1000 points have a Delaunay triangulation in 1-sheeted covering.
It is recommended to run this example only when compiled in release mode because of the relatively large number of points.
File: examples/Periodic_3_triangulation_3/large_point_set.cpp
#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Periodic_3_triangulation_traits_3.h>
#include <CGAL/Periodic_3_Delaunay_triangulation_3.h>
#include <CGAL/Random.h>
#include <CGAL/point_generators_3.h>
#include <CGAL/Timer.h>
#include <iostream>
#include <vector>
typedef CGAL::Exact_predicates_inexact_constructions_kernel K;
typedef CGAL::Periodic_3_triangulation_traits_3<K> GT;
typedef CGAL::Periodic_3_Delaunay_triangulation_3<GT> PDT;
typedef PDT::Point Point;
int main()
{
CGAL::Timer t;
typedef CGAL::Creator_uniform_3<double, Point> Creator;
CGAL::Random random(7);
CGAL::Random_points_in_cube_3<Point, Creator> in_cube(.5, random);
int n = 10000;
std::vector<Point> pts;
PDT PT1, PT2, PT3;
// Generating n random points
for (int i=0 ; i < n ; i++) {
Point p = *in_cube;
in_cube++;
pts.push_back(Point(p.x()+.5,p.y()+.5,p.z()+.5));
}
// Standard insertion
t.start();
for (int i=0 ; i < n ; i++) {
PT1.insert(pts[i]);
}
t.stop();
std::cout<<" Time: "<<t.time()<<" sec. (Standard insertion)"<<std::endl;
t.reset();
// Iterator range insertion using spatial sorting but no dummy points
t.start();
PT2.insert(pts.begin(), pts.end()); // third parameter defaults to false
t.stop();
std::cout<<" Time: "<<t.time()<<" sec. (with spatial sorting)"<<std::endl;
t.reset();
// Iterator range insertion using spatial sorting and dummy point heuristic
t.start();
PT3.insert(pts.begin(), pts.end(), true);
t.stop();
std::cout<<" Time: "<<t.time()<<" sec. (Dummy point heuristic)"<<std::endl;
return 0;
}
37.6.5 Geometric Access
There might be applications that need the geometric primitives of a triangulation as an input but do not require a simplicial complex. For these cases we provide the geometric iterators that return only the geometric primitives fulfilling some properties. In the following example we use the Periodic_triangle_iterator with the option UNIQUE_COVER_DOMAIN. This means that only those triangles are returned that have a non-empty intersection with the original domain of the 1-sheeted covering space, see Figure 37.4. The Periodic_triangle is actually a three-dimensional array of point-offset pairs. We check for all three entries of the periodic triangle whether the offset is (0,0,0) using the method is_null. If so, we convert the periodic triangle to a PK::Triangle_3, which requires exact constructions to be exact.
File: examples/Periodic_3_triangulation_3/geometric_access.cpp
#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Periodic_3_triangulation_traits_3.h>
#include <CGAL/Periodic_3_Delaunay_triangulation_3.h>
typedef CGAL::Exact_predicates_inexact_constructions_kernel K;
typedef CGAL::Periodic_3_triangulation_traits_3<K> PK;
typedef CGAL::Periodic_3_Delaunay_triangulation_3<PK> P3DT3;
typedef PK::Point_3 Point;
typedef PK::Triangle_3 Triangle;
typedef P3DT3::Periodic_triangle Periodic_triangle;
typedef P3DT3::Periodic_triangle_iterator Periodic_triangle_iterator;
typedef P3DT3::Iterator_type Iterator_type;
int main() {
P3DT3 T;
T.insert(Point(0,0,0));
T.insert(Point(0,0,0.5));
T.insert(Point(0,0.5,0.5));
T.insert(Point(0.5,0,0.5));
Periodic_triangle pt;
Triangle t_bd;
// Extracting the triangles that have a non-empty intersection with
// the original domain of the 1-sheeted covering space
for (Periodic_triangle_iterator ptit = T.periodic_triangles_begin(P3DT3::UNIQUE_COVER_DOMAIN);
ptit != T.periodic_triangles_end(P3DT3::UNIQUE_COVER_DOMAIN); ++ptit) {
pt = *ptit;
if (! (pt[0].second.is_null() && pt[1].second.is_null() && pt[2].second.is_null()) ) {
// Convert the current Periodic_triangle to a Triangle if it is
// not strictly contained inside the original domain.
// Note that this requires EXACT constructions to be exact!
t_bd = T.construct_triangle(pt);
}
}
}
37.7 Design and Implementation History
In 2006, Nico Kruithof started together with Monique Teillaud the Periodic_3_triangulation_3 package.
In 2007, Manuel Caroli continued work on the Periodic_3_triangulation_3 package together with Monique Teillaud.